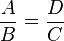SEMANA DEL 6 AL 10 DE MAYO

SEMANA DE EVALUACIONES BIMESTRALES 
ver video AQUÍ

En esta publicación encontrará el repaso de algunos temas vistos, que lo prepararán  para las evaluaciones BIMESTRALES Y SEMESTRALES. también para procesos de nivelación del segundo  periodo.

En algunos grados hay introducción a temas nuevos.

Matemática de sexto grado (2 videos)

Evaluación 6-1: Viernes 10 de mayo

Evaluación 6-2: Lunes 6 de mayo

Evaluación 6-3: Viernes 10 de mayo

SOLUCIÓN DE PROBLEMAS DE FRACCIONES: 

1. Operación de multiplicación y simplificación  Ver video1 haciendo clic AQUÍ

2. Operaciones de suma,resta, multiplicación y división de fracciones. Ver video2. Haga clic AQUÍ

Repaso de conceptos:

___________________________________________________________________________

 ___________________________________________________________________________

TALLER

2. b. Mónica empaca dulces en cajas de media docena cada una. Si completó siete cajas y ocupó cinco espacios más de otra caja, ¿qué fracción de las cajas utilizó? Exprésa esa cantidad como número mixto.

3.  Francisco compró tres pizzas para una fiesta y dividió cada una en seis partes iguales. Al terminar la fiesta, recogió los platos y vio que habían sobrado ocho porciones. Era necesario comprar las 3 pizzas?. explique.

4.

Unos más 

_________________________________________________________________

MATEMÁTICA DE SÉPTIMO GRADO( 7 videos)

Evaluaciones: 

Lunes 6 de mayo:  operaciones de suma y resta de fracciones: Ver video1 AQUÍ

Jueves 9 de mayo: Operaciones combinadas con  fraccionarios. Pagina 15. Ver video2 haciendo clic AQUÍ

     

1. SOLUCIÓN DE PROBLEMAS DE FRACCIONES: Repaso de sexto grado

    a.  Operación de multiplicación y simplificación  Ver video3 haciendo clic AQUÍ

    b. Operaciones de suma,resta, multiplicación y división de fracciones. Video4. Haga clic AQUÍ
2. NUMEROS RACIONALES: CONCEPTO. Ver video5 AQUÍ

COMPARACIÓN DE FRACCIONES

Evaluación lunes 6: sumar o restar fracciones ver video6 AQUÍ

OPERACIONES DE SUMA, RESTAS, MULTIPLICACIÓN Y DIVISIÓN CON NÚMEROS  FRACCIONARIOS POSITIVOS Y NEGATIVOS (los números racionales Q)

EVALUACIÓN FINAL DE PERIODO JUEVES 16 DE MAYO

Modelo de evaluación de números racionales: ver video7 AQUÍ

PRÓXIMA SEMANA: 

Nivelaciones y TEMA, operaciones COMBINADAS con números racionales. Ver video5 AQUÍ

Operaciones combinadas con paréntesis.  Ver video haciendo clic AQUÍ  y también  AQUÍ

Orden el las operaciones combinadas. Ver video haciendo clic AQUÍ 

Operaciones con números grandes. Ver video haciendo clic AQUÍ

Con llaves y corchetes. Ver video AQUÍ

      DIBUJO GEOMÉTRICO SÉPTIMO GRADO

Encuentre el perímetro y el área de cada figura individual con las cuales está compuestas la figura1 y figura2. También encuentre el perímetro y el área total de cada figura.

Nota: Para la figura 2  el área de la figura total, debe encontrarla de dos formas diferentes.

1. Sumando el valor de las áreas individuales

2. por la fórmula de área de la figura total.

FIGURA 1

FIGURA 2

       Dibujo geométrico grado octavo (2 videos)

Recuerde que el 8 de mayo hay evaluación y trabajo de polígonos. Taller páginas 10 y 11
tema nuevo:
 Figuras semejantes. ver video AQUÍ. 

Aplicación de teorema de THALES. Ver video AQUÍ

El concepto de semejanza puede generalizarse mas allá de los polígonos.Hablamos, entonces, de figuras semejantes.

Decimos que dos figuras son semejantes si la proporción entre la distancia de dos puntos cualesquiera y la distancia de sus puntos homólogos se mantiene.

Así pues, dos figuras semejantes tienen la misma forma, pero distinto tamaño.

Para trabajar el concepto de semejanza entre triángulos se debe tener en cuenta el teorema                                                                  

La escala a la que se ha reproducido un dibujo se indica al pie de éste y se expresa mediante un cociente cuyo dividendo es la unidad.

Así, la escala 1 : 200 significa que una unidad de longitud del dibujo representa 200 unidades de estas mismas unidades en la realidad.

Ejemplos de representaciones hechas a escala serían los planos, las maquetas o los mapas.

A menudo, en el caso de los mapas, la escala se indica de forma gráfica, tal y como muestra la figura.

PRACTICA

ALGEBRA DE OCTAVO

División de polinomios

Regla de Ruffini  o división sintética: Teoría y Ejemplos. Ver video haciendo clic AQUÍ

Teorema del residuo. Ver video haciendo clic AQUÍ

DIBUJO GEOMÉTRICO DE NOVENO GRADO

Recuerde que el 8 de mayo hay evaluación y tareas sobre círculos y circunferencias. Página  2 a la 7 del módulo.

POLÍGONOS

Polígonos irregulares

Para calcular el área de un polígono irregular, podemos descomponerlo en el menor número posible de figuras cuyas áreas sepamos calcular. A menudo, lo más fácil es descomponerlo en triángulos.